サービス内容
私達が持っている知識と経験を生かして、様々なアプリケーションや研究に役に立ちたい。個人的な気配り、専門的なコンサルティングと同様に最新のテクノロジーへのアクセスを提供できると信じています。ご相談、ご質問がございましたら、お問い合わせください。
光は波とし考えると、干渉や回折などの性質が波動光学で説明できます。特に、眼光学において、波面収差と瞳孔径を用いることで、さまざまな光学特性を正確に求められることが重要です。焦点を持つ光学系についてフーリエ変換作用で簡単に解析できるフーリエ光学を以下のようにわかりやすく説明します。

ホイヘンスの原理
ホイヘンスの原理は、Fig. 1 のように点光源 $S$ があるときに、波は全ての方向に伝搬され、同位相面を元の波の波面(primary wavefront)を作る。そのとき波面上のある点では、それぞれの点が中心となって新しい波源になる波を発生させていると考える。ここで発生する波を素元波(secondary wavelets)と呼ぶ。このように、無数に存在する素元波と素元波が接する面が新しい波面(包絡面)(new wavefront)を形成する。

Fig. 1. ホイヘンスの原理による点光源の伝搬
点光源の場合、形成される球面波(英:spherial wave)を次のように表される。
\[
\psi_{\text{Sphere}} = \displaystyle\frac{e^{-jkr}}{r}
\]
ここで、$\psi_{\text{Sphere}}$ は球面波、$j$ は虚数単位、$r$ は点光源から観測点までの距離、$k$ は波数であり、次式に定義され、$\nu$ は波の周波数、$c$ は真空中での伝搬速度、$\lambda$ は波長である。
\[
k=\displaystyle\frac{2\pi \nu}{c} = \displaystyle\frac{2\pi}{\lambda}
\]
球面波の特徴として、振幅 $1/r$、位相 $kr$、光源からの距離が大きくなるにしたがって減衰し、$r\to\infty$ の極限で振幅は $0$ となる。具体的に言えば、振幅は光源からの距離に反比例する。また、光の強さ(強度)は、振幅の2乗であるため、距離の2乗に半比例する。
つまり、球面波は $e^{-jkr}$ の波、オイラーの公式を利用して、実部のみの場合は $\cos(kr)$ の波が光源から伝搬して、光源から離れると強度が減衰するの物理的な意味を持つ。さらに拡張すると、球面波は、点光源から発生、もしくは逆に、一点に向かって収束する球状の波動のことである。

波動方程式
光は電磁波の一種であり、マクスウェルの方程式から容易に導き出せるベクトル波動方程式によって伝搬される。
最も基礎的な回折問題は、単にこのように任意の点から別の点に波を伝搬する手法を決定することである。波動光学において、一般的なスカラー波動方程式は次のように記述することができる。
\[
\nabla^2 u = \displaystyle\frac{1}{c^2}\frac{\partial^2u}{\partial t^2}
\]
ここで、$\nabla^2$ はラプラス作用素、$u$は空間と時間の関数であり、二階空間微分と二階時間微分は恒等的に等しいを表している。
つまり、波動方程式の解としては次式の形で成り立つ。
\[
u(x,y,z,t)=\psi(x,y,z)e^{-j2\pi \nu t}
\]
つまり、時間的には角周波数 $\omega =2\pi \nu$ で調和振動するもので、その振幅が空間(位置)に依存するという解である。
この解をスカラー波動方程式に代入すると、次の式が得られる。
\[
\nabla^2\psi + k^2\psi = 0
\]
この式は、ヘルムホルツ方程式という。このようなヘルムホルツ方程式を満たす解、すなわち境界を持たない自由空間における解としてグリーンの定理で求められ、グリン関数が知られている。
\[
G(\operatorname{r}-\operatorname{r^\prime}) = \displaystyle{\frac{e^{-jk|\operatorname{r}-\operatorname{r^\prime}|}}{|\operatorname{r}-\operatorname{r^\prime}|}}
\]
ここで、$|\operatorname{r}-\operatorname{r^\prime}|$ は自由空間にある二つの点の距離を表し、ベクトルの形とされる。つまり、ヘルムホルツ方程式の一つの解としては、球面波であることがわかる。

フレネル・キルヒホッフの回折理論
波動方程式から求められた解が球面波でかることを示したが、実際の光学系では、点光源ではなく、光を開口に通過して焦点面に伝搬する。
そこで、平行光が開口を通過する場合を考える。
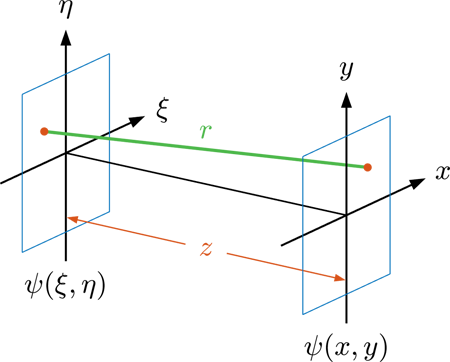
Fig. 2. 光伝搬の座標系
Fig. 2 に示すように、開口面 $\psi(\xi,\eta)$ にあるとき、開口面から距離 $z$ の位置にある観測スクリーン $\psi(x,y)$ 上に伝搬するとき、その伝搬された光をキルヒホッフの回折理論に基づいて次式で与えられる。
\[
\psi(x,y) = \displaystyle\iint\limits_{\text{Aperture}}\!\!\psi(\xi,\eta)~K(x,y,\xi,\eta)~\displaystyle\frac{e^{-jkr(x,y,\xi,\eta)}}{r(x,y,\xi,\eta)}~d\xi~d\eta
\]
ここで、$K(x,y,\xi,\eta)$は光軸の傾斜係数であり、近軸の場合、光が開口の中央を通過する光線に限定させ、この傾斜係数は一定であり、積分から取り除くことができる。また、開口の大きさと比較してスクリーンまでの距離$z$が十分大きいとき、$1/r\approx 1/z$ に近似する。よって、キルヒホッフの回折理論の式は次のように簡略化することができる。
\[
\psi(x,y) = \displaystyle\frac{K}{z} \iint\limits_{\text{Aperture}}\!\!\psi(\xi,\eta)~e^{-jkr(x,y,\xi,\eta)}~d\xi~d\eta
\]
次ぎに、点 $(\xi,\eta)$ から点 $(x,y)$ までの距離が $r$ で表し、次のように書ける。
\[
r(x,y,\xi,\eta) = \sqrt{(x-\xi)^2 + (y-\eta)^2 + z^2}
\]
$R^2 = x^2 + y^2 + z^2$ とおくと、また、$|(\xi^2 + \eta^2) - 2(\xi x + \eta y)|\ll R^2$ の条件を満たせば、二項級数の一次近似を適用できる。よって、$r$ は次式のように近似できる。
\[
r(x,y,\xi,\eta) \approx R + \displaystyle\frac{\xi^2+\eta^2}{2R} - \frac{\xi x+\eta y}{R}
\]
キルヒホッフの回折理論の式に代入すると、次の式が得られる。一般に、この条件下の回折はフレネル・キルヒホッフの回折理論と呼ばれる。
\[
\psi(x,y) = \displaystyle\frac{Ke^{-jkR}}{z} \iint\limits_{\text{Aperture}}\!\!\psi(\xi,\eta)~e^{-jk\left(\frac{\xi^2+\eta^2}{2R} - \frac{\xi x+\eta y}{R}\right)}~d\xi~d\eta
\]

レンズのフーリエ変換作用
平行光 $P$ が開口を通過する光にレンズを配置し、レンズの焦点面をスクリーン上に形成された回折パターンの解を考えてみよう(Fig. 3 参照)。レンズのサイズは有限であり、それを開口(瞳関数)を $A(\xi,\eta)$、レンズの焦点距離を $f$とする。
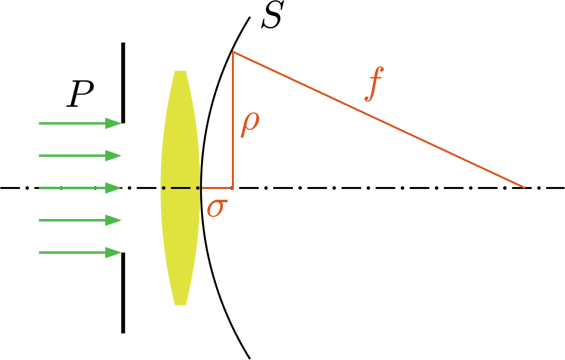
Fig. 3. レンズと焦点面の座標系
レンズは、屈折現象を利用して開口に照射された光を特定の一点に集結するように表面の曲率が設計されている。このように、光を一点に集結する場合、ホイヘンスの原理に基づいて、レンズは収差がない理想的なレンズとおくと、球面波 $S$ を形成される。また、焦点は光軸にあるため、$z = R = f$ となる。Fig. 3 に示すように、形成された球面波上の高さ $\rho$ のときの距離 $\sigma$ は $\rho^2\ll f^2$ の条件下で次のように近似できる。
\[
\sigma = f - \sqrt{f^2 - \rho^2} \approx \displaystyle \frac{\rho^2}{2f}
\]
レンズ面 $(\xi,\eta)$ の座標系におくと、$\rho^2 = \xi^2 + \eta^2$ であり、レンズによって導入される位相変化は $\phi = k\sigma$ になる。この位相変化量をフレネル・キルヒホッフの回折理論の式に追加され、フレネル・キルヒホッフの回折理論の第1項と直接打ち消されている。よって、レンズの焦点面にある振幅分布は次のようにまとめられる。
\[
\psi(x,y) = \displaystyle\frac{Ke^{-jkf}}{f} \iint\limits_{\text{Aperture}}\!\! \psi(\xi,\eta)~e^{\frac{jk}{f}\left(\xi x+\eta y\right)}~d\xi~d\eta
\]
以上のように、レンズの焦点面の回折パターンを決定する積分は、フーリエ変換作用として使用される。
また、フーリエ変換作用を記号として表すことによって、レンズの焦点面にある振幅分布は非常にシンプルに表現できる。
\[
\psi(x,y) \propto \mathcal {F}~\{\psi(\xi,\eta)\}
\]
上記に説明したように、レンズは収差がない理想的なレンズにおいては $\psi(\xi,\eta)$ の振幅分布を開口関数(開口部を $1$、遮蔽部を $0$ )として、位相分布を $0$ としてのフーリエ変換作用となる。理想的なレンズではないときには、収差による位相分布ズレとしてのフリエー変換作用とするだけで簡単に求められる。